Teoria Carolana – kalendarz spiralny cz.3. “Właściwości ciągu fibonacciego”
Leonardo Fibonacci
żył w latach 1175-1250, był włoskim matematykiem pochodzącym z Pizy. Uważał 0 za pierwszą liczbę naturalną, zajmował się rozkładem liczby na czynniki pierwsze. To dzięki niemu posługujemy się cyframi arabskimi i to właśnie on podał wzór określający kolejne wyrazy ciągu Fibonacciego.
W tym ciągu liczb naturalnych pierwsze dwa wyrazy ciągu są równe 1 a każdy następny wyraz (zwany liczbą Fibonacciego) powstaje jako suma dwóch poprzednich, czyli 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8 itd. aż do nieskończoności: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
Jeżeli podzielimy przez siebie dowolne, kolejne dwa wyrazy ciągu Fibonacciego, np. 987 : 610; 89 : 55 to stosunek tych liczb będzie równy zawsze tej samej liczbie, równej w przybliżeniu 1.618. Im większe wyrazy ciągu podzielimy, tym dokładniejsze przybliżenie tej liczby uzyskamy. Liczbę tę nazywa się “złotą liczbą” i oznacza grecką literą φ (czyt. “fi”). Stosunek tego podziału określa się również mianem “złotego podziału” lub “Boskiej proporcji”. Warto również wspomnieć o spirali Fibonacciego, szczególnym przypadku tzw. złotej spirali, której szerokość zwiększa się (lub zmniejsza) o 90° dokładnie φ razy (czyli o “złotą liczbę”) (źródło interia.pl).
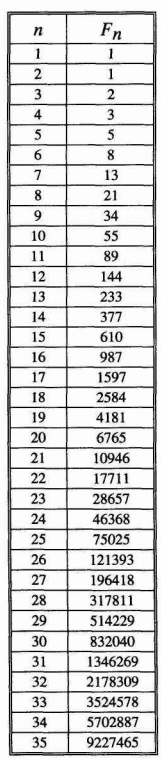
Fascynujące właściwości ciągu fibonacciego:
- suma każdych kolejnych “10-ciu” wyrazów ciągu Fn jest podzielna przez “11”,
- każdy trzeci wyraz ciągu jest podzielny przez 2, czwarty przez 4, piąty przez 5 itd.,
- 1 i 144 to jedyne wyrazy ciągu, z których wyciąga się pierwiastek bez reszty,
- końcowe numery ciągu fibbo powtarzają się co “60”. Ostatnie dwie co 300, ostatnie trzy co 1500, cztery co 15000 itd.,
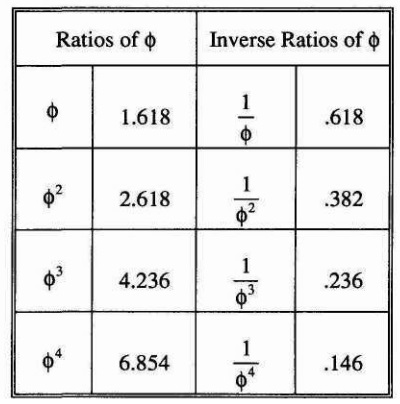
- inwersja liczby fi (1/ fi ) zachowuje proporcje liczb “fibo”, nazywane często “liniami/poziomami życia”, tzw. złota seria: 0.236; 0.382; 0.618; 1 ; 1.618; 2.618 ; 4.236… (tabela. 2.)
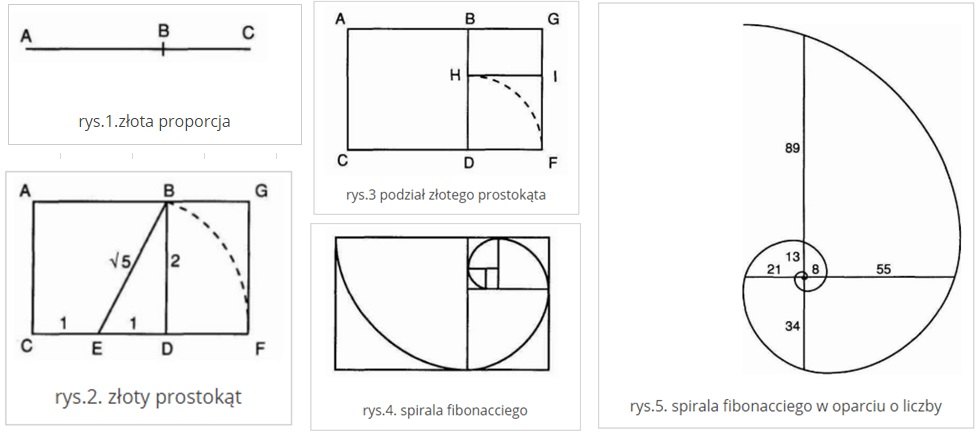
Geometria liczby “fi” (rysowanie spirali fibonacciego)
- złota proporcja AB/BC = AC/AB = fi= 1.618 (rys.1.),
- złoty prostokąt ABCD gdzie CF/GF = fi oraz mniejszy prostokąt BGDF spełnia fi = GF/DF (rys.2.),
- złoty prostokąt DHIF i mniejszy BGIH również spełniają złotą proporcje (rys.3),
- złota spirala łączy punkty każdego złotego prostokąta (rys.4),
- przykład spirali w oparciu o wybrane wyrazy ciągu fibonacciego (rys.5.).








Świetny artykuł! Inwestowanie i matematyka… ale również przyroda – to wszystko ma głęboki sens.